lunes, 17 de enero de 2011

Teoría de supercuerdas

El objetivo de esta publicacion, es mostrar el ultimo avance de la fisica cuantica (que es la comprension del movimiento de los cuerpos a nivel atomico). Este teorema se esta estudiando y desarrollando. Es llamado Teorema de Supercuerdas.

La teoría de supercuerdas es un esquema teórico para explicar todas las partículas y fuerzas fundamentales de la naturaleza en una sola teoría que modela las partículas y campos físicos como vibraciones de delgadas cuerdas supersimétricas que se mueven en un espacio-tiempo de más de 4 dimensiones.
Una de las motivaciones esgrimidas por los teóricos de las supercuerdas es que el esquema es una de las mejores teorías candidatas para formular una teoría cuántica de la gravedad. La teoría de las supercuerdas es una taquigrafía de la teoría supersimétrica de cuerdas porque, a diferencia de la teoría de cuerdas bosónica, esta es la versión de la teoría de cuerdas que, mediante la supersimetría, incorpora a los fermiones.
La teoría de las supercuerdas comprende cinco teorías o formulaciones alternativas de teorías de cuerdas, combinadas en la que se han introducido requerimientos de supersimetría. El nombre teoría de cuerdas se usa actualmente como sinónimo ya que todas las teorías de cuerdas ampliamente estudiadas son, de hecho, teorías de supercuerdas.
La idea fundamental es que en realidad son cuerdas que vibran en resonancia a una frecuencia de la longitud de Planck y en donde el gravitón sería una cuerda de espín 2 y masa nula.
Recientemente se ha podido probar que varias de estas formulaciones son equivalentes y tras todas ellas podría existir una teoría unificada o teoría del todo. Las cinco teorías existentes no serían más que casos límite particulares de esta teoría unificada, denominada provisionalmente como Teoría M. Esta teoría M intenta explicar a la vez todas las partículas subatómicas existentes y unificar las cuatro fuerzas fundamentales de la naturaleza. Define el universo formado por multitud de cuerdas vibrantes, ya que es una versión de la teoría de cuerdas que incorpora fermiones y la supersimetría.
El principal problema de la física actual es poder incorporar la fuerza de la gravedad tal y como la explica la teoría de la relatividad general al resto de las fuerzas físicas ya unificadas. La teoría de las supercuerdas sería un método de unificación de dichas teorías. La teoría está lejos de estar acabada y perfilada, ya que hay muchísimas variables sin definir, por lo que existen varias versiones de la misma.

 Antecedentes

El problema de fondo en la física teórica es armonizar la teoría de la relatividad general, donde se describen la gravitación y las estructuras a gran escala (estrellas, galaxias, cúmulos), con la mecánica cuántica, donde se describen las otras tres fuerzas fundamentales que actúan a nivel atómico.
El desarrollo de la teoría cuántica de campos de una fuerza invariable resulta en infinitas (y útiles) probabilidades. Los físicos han desarrollado técnicas matemáticas de renormalización para eliminar esos infinitos de tres de las cuatro fuerzas fundamentales -electromagnetismo, nuclear fuerte y nuclear débil- pero no de la gravedad. El desarrollo de la teoría cuántica de la gravedad debe, por lo tanto, venir de diferente manera que de los usados para las otras fuerzas.
La idea básica es que los constituyentes fundamentales de la realidad son cuerdas de una longitud de Planck (cercano a 10−35 m) que vibran a frecuencias de resonancia. Cada cuerda en teoría tiene una única resonancia, o armonía. Diferentes armonías determinan diferentes fuerzas fundamentales. La tensión en la cuerda es del orden de las fuerzas de Planck (1044 N). El gravitón (nombre propuesto para la partícula que lleve la fuerza gravitacional), por ejemplo, es predicha por la teoría que sea una cuerda con amplitud cero. Otra idea clave de la teoría es que no pueden ser detectadas diferencias mensurables entre cuerdas que recapitulan sobre dimensiones pequeñas en sí mismas y muchas que se mueven en grandes dimensiones (p.e. que afectan a una dimensión de tamaño R iguales a una de tamaño 1/R). Las singularidades son evitadas porque las consecuencias observables del "gran colapso" nunca alcanzan el tamaño cero. De hecho puede el universo comenzar un pequeño "gran colapso" de procesos, la teoría de cuerdas dice que el universo nunca puede ser más pequeño que el tamaño de una cuerda, a ese punto podría comenzar a expandirse.

 El problema de las dimensiones

Aunque el universo físico observable tiene tres dimensiones espaciales y una dimensión temporal, nada prohíbe a una teoría describir un universo con más de cuatro dimensiones, especialmente si existe un mecanismo de "inobservabilidad aparente" de las dimensiones adicionales. Ése es el caso de las teoría de cuerdas y la teoría de supercuerdas que postulan dimensiones adicionales compactificadas y que sólo serían observables en fenómenos físicos que involucran altísimas energías. En el caso de la teoría de supercuerdas, la consistencia de la propia teoría requiere un espacio-tiempo de 10 ó 26 dimensiones. El conflicto entre la observación y la teoría se resuelve compactando las dimensiones que no se pueden observar en el rango de energías habituales. De hecho, la teoría de supercuerdas no es la primera teoría física que propone dimensiones espaciales extra; a principios del siglo XX se propuso una teoría geométrica del campo electromagnético y gravitatorio conocida como teoría de Kaluza-Klein que postulaba un espacio-tiempo de 5 dimensiones. Posteriormente la idea de Kaluza y Klein se usó para postular la teoría de la supergravedad de 11 dimensiones que también utiliza la supersimetría.
La mente humana tiene dificultad visualizando dimensiones mayores porque solo es posible moverse en 3 dimensiones espaciales. Una manera de tratar con esta limitación es no intentando visualizar dimensiones mayores del todo sino simplemente pensando, al momento de realizar ecuaciones que describan un fenómeno, que se deben realizar más ecuaciones de las acostumbradas. Esto abre las interrogantes de que estos 'números extra' pueden ser investigados directamente en cualquier experimento (donde se mostrarían resultados en 1, 2, 2+1 dimensiones a científicos humanos). Así, a su vez, aparece la pregunta de si este tipo de modelos que se investigan en este modelado abstracto (y aparatos experimentales potencialmente imposibles) puedan ser considerados 'científicos'. Las formas de seis dimensiones de Calabi-Yau pueden contar con dimensiones adicionales por la teoría de supercuerdas.
Una teoría que la generaliza es la teoría de branas, en donde las cuerdas son sustituidas por constituyentes elementales de tipo "membrana", de ahí su nombre. La existencia de 10 dimensiones es matemáticamente necesaria para evitar la presencia de taquiones, partículas más rápidas que la luz, y los "fantasmas", partículas con probabilidad de existencia nula.
La Teoría de las Supercuerdas se puede explicar con la Física Racional a través de la Mecánica de Fluidos, sin necesidad de recurrir a espacio superiores a tres dimensiones. A este fin, basta considerar a las cuerdas como hilos de remolinos, que hay en un fluido ideal en agitación (fluido magnético). Los remolinos según su espín serán fermiones o bosones, correspondientes a las partículas subatómicas, con los remolinos también explicamos los agujeros negros, las cargas eléctricas, así como la formación de masa en el campo, a la vez que nos da explicación a las cuatro fuerzas de la naturaleza. Todo esto constituye una nueva teoría denominada Teoría del Cladín, y hay colgados de ella varios artículos en Internet.

 Cantidad de teorías de supercuerdas

Los físicos teóricos fueron perturbados por la existencia de cinco diferentes teorías de cuerdas. Esto aconteció bajo la denominada segunda revolución de supercuerdas en los años 1990 donde fueron postuladas las 5 teorías de cuerdas, siendo diferentes casos límite de una única teoría: la teoría M.

Teoría de Cuerdas
TiposDimensiones EspacialesDetalles
Bosonica26Solo bosones no fermiones, significa solo fuerzas, no materia, con cuerdas abiertas y cerradas; mayor defecto: una partícula con masa imaginaria llamada taquión
I10Supersimetría entre fuerza y materia, con cuerdas abiertas y cerradas, libre de taquiones, grupo de simetría SO(32)
IIA10Supersimetría entre fuerza y materia, solo con cuerdas cerradas, libre de taquiones, fermiones sin masa que giran a ambas direcciones
IIB10Supersimetría entre fuerza y materia, solo con cuerdas cerradas, libre de taquiones. fermiones sin masa que giran en una sola dirección
HO10Supersimetría entre fuerza y materia, solo con cuerdas cerradas, libre de taquiones, heterótica, difieren entre cuerdas de movimiento derecho e izquierdo, grupo de simetría es SO(32)
HE10Supersimetría entre fuerza y materia, solo con cuerdas cerradas, libre de taquiones, heterótica, difieren entre cuerdas de movimiento derecho e izquierdo, grupo de simetría E8×E8

Las cinco teorías de supercuerdas consistentes son:
  • La teoría de cuerdas Tipo I tiene una supersimetría en sentido diez-dimensional (16 supercargas). Esta teoría es especial en el sentido de que está basada en una orientación abierta y cerrada, mientras el resto se basan en cuerdas con orientaciones cerradas.
  • La teoría de cuerdas Tipo II tiene dos supersimetrías en sentido de 10 dimensiones (32 supercargas). Hay de hecho dos tipos de cuerdas Tipo II llamadas tipo IIA y IIB. Difieren principalmente en el hecho que la teoría IIA es no quiral (conservando la paridad), mientras que la teoría IIB es quiral (violando la paridad).
  • La teoría de la cuerda heterótica está basada en un peculiar híbrido de una supercuerda de tipo I y una cuerda bosónica. Hay 2 tipos de cuerdas heteróticas que difieren en su diez-dimensional grupo de gauge: la cuerda heterótica E8×E8 y la SO(32). (el nombre heterótico SO(32) es un poco inexacta en el SO(32) del Grupo de Lie, las teorías son un cociente de Spin(32)/Z2 que no es equivalente a SO(32).)
Las teorías quirales de gauge pueden ser inconsistentes en sus anomalías. Esto ocurre cuando un bucle del Diagrama de Feynman causa un rompimiento de la mecánica cuántica de la simetría de gauge. Anulando anomalías se limita a las posibles teorías de cuerdas.

 Integrando relatividad general con mecánica cuántica

La relatividad general normalmente se refiere a situaciones que envuelven objetos masivos grandes en lejanas regiones del espacio-tiempo donde la mecánica cuántica se reserva para escenarios a escala atómica (regiones pequeñas de espacio-tiempo). Las dos son muy difícilmente usadas juntas, y el caso más común en donde se combina su estudio son los agujeros negros. Teniendo "picos de densidad" o máximo cantidades de materia posible en el espacio, y un área muy pequeña, las dos deben ser usadas en sincronía para predecir condiciones en ciertos lugares; aun cuando son usados juntos, las ecuaciones se desmoronan y brindan respuestas imposibles, tales como distancias imaginarias y menos de una dimensión.
El mayor problema con su congruencia es que, a dimensiones menores a las de Planck, la relatividad general predice una certeza, una superficie fluida, mientras que la mecánica cuántica predice una probabilidad, una superficie deformada; que no son compatibles. La teoría de supercuerdas resuelve este requerimiento, remplazando la idea clásica de partículas puntuales con bucles. Esos bucles tendrían un diámetro promedio de una longitud de Planck, con variaciones extremadamente pequeñas, que ignora completamente las predicciones de la mecánica cuántica a dimensiones menores a las de Planck, y que para su estudio no toma en cuenta esas longitudes.

 Falsacionismo y teoría de supercuerdas


La Teoría de cuerdas o la Teoría M podrían no ser falsables, según algunos críticos.[1] [2] [3] [4] ¿Habría que revisar el concepto de qué se considera científico o habría que desechar el falsacionismo propuesto por Popper como requisito para que una teoría pueda ser considerada científica? Si así fuera, ¿cómo sería posible delimitar con objetividad qué es ciencia y qué pseudociencia?.
Muchos científicos han declarado su preocupación de que la Teoría de cuerdas no sea falsable y que además, carezca de poder predictivo, y como tal, y siguiendo las tesis del filósofo de la ciencia Karl Popper, la Teoría de cuerdas sería equivalente a una pseudociencia.[5] [6] [7] [8] [9] [10]
Tal y como se entiende en la actualidad, tiene un número gigantesco de posibles soluciones.[11]
El filósofo de la ciencia Mario Bunge ha manifestado recientemente:
  • La consistencia, la sofisticación y la belleza nunca son suficientes en la investigación científica.
  • La Teoría de cuerdas es sospechosa (de pseudociencia). Parece científica porque aborda un problema abierto que es a la vez importante y difícil, el de construir una teoría cuántica de la gravitación. Pero la teoría postula que el espacio físico tiene seis o siete dimensiones, en lugar de tres, simplemente para asegurarse consistencia matemática. Puesto que estas dimensiones extra son inobservables, y puesto que la teoría se ha resistido a la confirmación experimental durante más de tres décadas, parece ciencia ficción, o al menos, ciencia fallida.
  • La física de partículas está inflada con sofisticadas teorías matemáticas que postulan la existencia de entidades extrañas que no interactúan de forma apreciable, o para nada en absoluto, con la materia ordinaria, y como consecuencia, quedan a salvo al ser indetectables. Puesto que estas teorías se encuentran en discrepancia con el conjunto de la Física, y violan el requerimiento de falsacionismo, pueden calificarse de pseudocientíficas, incluso aunque lleven pululando un cuarto de siglo y se sigan publicando en las revistas científicas más prestigiosas.
La crítica principal de que es objeto la Teoría de cuerdas es de que sea, fundamentalmente, imposible de falsear, debido a su naturaleza intrínseca: tiene la suficiente flexibilidad matemática como para que sus parámetros se puedan moldear para encajar con cualquier tipo de realidad observada.[1] [2]
Para ilustrar la confusa situación que domina este campo de investigación, baste citar el reciente escándalo Bogdanov, dos hermanos que consiguieron publicar en prestigiosas revistas científicas teorías absurdas y carentes de sentido. El físico alemán Max Niedermaier concluyó que se trataba de pseudociencia, escrita con una densa jerga técnica, para evitar el sistema de revisión por pares de la física teórica. Según el físico-matemático John Baez, su trabajo "es una mezcolanza de frases aparentemente plausibles que contienen las palabras técnicas correctas en el orden aproximadamente correcto. Pero no hay lógica ni cohesión en lo que escriben." Según el físico Peter Woit en la prestigiosa revista Nature: "El trabajo de los Bogdanoff resulta significativamente más incoherente que cualquier otra cosa publicada. Pero el creciente bajo nivel de coherencia en todo el campo les permitió pensar que habían hecho algo sensato y publicarlo."[13]

 Véase también

 Notas

  1. ↑ a b Smolin, Lee. Mariner Books, 2007. The trouble with Physics. ISBN 0-618-91868-X
  2. ↑ a b Woit, Peter. Basic Books, 2007. Not even wrong. ISBN 0-465-09276-4
  3. ↑ Sheldon Glashow & Paul Ginsparg, "Desperately Seeking Superstrings", Physics Today, mayo de 1986, p.7.
  4. ↑ Howard Georgi, en The New Physics,ed. Paul Davies, Cambridge University Press, Cambridge, 1989, p. 446
  6. ↑ P. Woit (Columbia University) String theory: An Evaluation,Feb 2001, e-Print: physics/0102051
  7. ↑ P. Woit, Is String Theory Testable? INFN Rome March 2007
  11. ↑ S. Kachru, R. Kallosh, A. Linde and S. P. Trivedi, de Sitter Vacua in String Theory, Phys.Rev.D68:046005,2003
  12. ↑ Mario Bunge. Skeptical Inquirer, July/Aug, 2006.

 Enlaces externos

Videos
Publicado por en No hay comentarios:

Teorema Fractal

El objetivo de esta publicacion es mostrar que se esta desarollando un calculo mas preciso y exacto que el calculo diferencial integral. El desarrollo de este teorema de fractal, tendra multiples aplicaciones a la ciencia.
Un fractal es un objeto semigeométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas.[1] El término fue propuesto por el matemático Benoît Mandelbrot en 1975 y deriva del Latín fractus, que significa quebrado o fracturado. Muchas estructuras naturales son de tipo fractal.
A un objeto geométrico fractal se le atribuyen las siguientes características:[2]
No basta con una sola de estas características para definir un fractal. Por ejemplo, la recta real no se considera un fractal, pues a pesar de ser un objeto autosimilar carece del resto de características exigidas.
Un fractal natural es un elemento de la naturaleza que puede ser descrito mediante la geometría fractal. Las nubes, las montañas, el sistema circulatorio, las líneas costeras[3] o los copos de nieve son fractales naturales. Esta representación es aproximada, pues las propiedades atribuidas a los objetos fractales ideales, como el detalle infinito, tienen límites en el mundo natural.

Contenido


 Introducción

La definición de fractal en los años 1970, dio unidad a una serie de ejemplos, algunos de los cuales se remontaban a un siglo atrás:

 Los ejemplos clásicos

Para encontrar los primeros ejemplos de fractales debemos remontarnos a finales del siglo XIX: en 1872 apareció la función de Weierstrass, cuyo grafo hoy en día consideraríamos fractal, como ejemplo de función continua pero no diferenciable en ningún punto.
sucesivos pasos de la construcción de la curva de Koch
Posteriormente aparecieron ejemplos con propiedades similares pero una definición más geométrica. Dichos ejemplos podían construirse partiendo de una figura inicial (semilla), a la que se aplicaban una serie de construcciones geométricas sencillas. La serie de figuras obtenidas se aproximaba a una figura límite que correspondía al que hoy llamamos conjunto fractal. Así, en 1904, Helge von Koch definió una curva con propiedades similares a la de Weierstrass: el copo de nieve de Koch. En 1915, Waclaw Sierpinski construyó su triángulo y, un año después, su alfombra.

Construcción de la alfombra de Sierpinski:
Menger 0.PNGMenger 1.PNGMenger 2.PNGMenger 3.PNGMenger 4.PNG
Paso 1 (semilla)Paso 2Paso 3Paso 4Paso 5

Estos conjuntos mostraban las limitaciones del análisis clásico, pero eran vistos como objetos artificiales, una "galería de monstruos", como los denominó Poincaré. Pocos matemáticos vieron la necesidad de estudiar estos objetos en sí mismos.[4]
En 1919 surge una herramienta básica en la descripción y medida de estos conjuntos: la dimensión de Hausdorff-Besicovitch.

 Los conjuntos de Julia

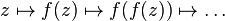Estos conjuntos, fruto de los trabajos de Pierre Fatou y Gaston Julia en los años 1920, surgen como resultado de la aplicación reiterada de funciones holomorfas z \mapsto f(z) \mapsto f(f(z)) \mapsto \ldots.
Analicemos el caso particular de funciones polinómicas de grado mayor que uno. Al aplicar sucesivas veces una función polinómica es muy posible que el resultado tienda a \infty. Al conjunto de valores de z \in C que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de Julia.
Estos conjuntos se representan mediante un algoritmo de tiempo de escape, en que cada pixel se colorea según el número de iteraciones necesarias para escapar. Suele usarse un color especial, a menudo el negro, para representar los puntos que no han escapado tras un número grande y prefijado de iteraciones.
Ejemplos de conjuntos de Julia para fc(z) = z2 + c
En negro, conjunto de Julia relleno asociado a fc, c=φ-2, donde φ es el número áureo
Conjunto de Julia relleno asociado a fc, c=(φ−2)+(φ−1)i =-0.4+0.6i
Conjunto de Julia relleno asociado a fc, c=-0.835-0.2321i
En negro, imagen del conjunto de Mandelbrot superpuesto con los conjuntos de Julia rellenos representados por algunos de sus puntos (en rojo los conjuntos de Julia conexos y en azul los no conexos).

 Familias de fractales: el conjunto de Mandelbrot

La familia de conjuntos de Julia {fc}, asociadas a la reiteración de funciones de la forma fc(z) = z2 + c presenta conjuntos de una variedad sorprendente.
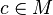Dicha familia tendrá especial relevancia al quedar parametrizada en un mapa de fractales, popularizado en los años 1980. llamado conjunto de Mandelbrot. Este conjunto M representa un mapa en que cada pixel, correspondiente a un valor del parámetro c \in \mathbb{C}, se colorea de modo que refleje una propiedad básica del conjunto de Julia asociado a fc. En concreto, c \in M si el conjunto de Julia asociado a fc es conexo.

 Características de un fractal

 Autosimilitud

Según B. Mandelbrot, un objeto es autosimilar o autosemejante si sus partes tienen la misma forma o estructura que el todo, aunque pueden presentarse a diferente escala y pueden estar ligeramente deformadas.[5]
Los fractales pueden presentar tres tipos de autosimilitud:
  • Autosimilitud exacta. este es el tipo más restrictivo de autosimilitud: exige que el fractal parezca idéntico a diferentes escalas. A menudo la encontramos en fractales definidos por sistemas de funciones iteradas (IFS).
Cuasiautosimilitud en el conjunto de Mandelbrot: al variar la escala obtenemos copias del conjunto con pequeñas diferencias.
  • Cuasiautosimilitud: exige que el fractal parezca aproximadamente idéntico a diferentes escalas. Los fractales de este tipo contienen copias menores y distorsionadas de sí mismos. Matemáticamente D.Sullivan definió el concepto de conjunto cuasiauto-similar a partir del concepto de cuasi-isometría. Los fractales definidos por relaciones de recurrencia son normalmente de este tipo.
  • Autosimilitud estadística. Es el tipo más débil de autosimilitud: se exige que el fractal tenga medidas numéricas o estadísticas que se preserven con el cambio de escala. Los fractales aleatorios son ejemplos de fractales de este tipo.

 Dimensión fractal y dimensión de Hausdorff-Besicovitch

Entre los fractales podemos encontrar ejemplos como curvas que llenan todo el plano. En ese caso, la dimensión topológica de la curva, que es uno, no nos informa sobre la forma en que esta ocupa el espacio ambiente. De modo general, podríamos preguntarnos cómo densamente un conjunto ocupa el espacio métrico que lo contiene. Los números que nos informan objetivamente de este tipo de cuestiones son:
  • La dimensión fractal. Las fórmulas que la definen tienen que ver con el recuento de las bolas necesarias para recubrir el conjunto o con el de cajas de una cuadrícula que contienen parte del conjunto, cuando las dimensiones de unas y otras tienden a cero. Podemos medir la dimensión fractal de objetos reales: líneas de la costa (1.2), nubes, árboles, etc, Con estas medidas podemos comparar objetos del mundo real con fractales generados por algoritmos matemáticos.
  • La dimensión de Hausdorff-Besicovitch. Tiene una definición más compleja que la de dimensión fractal. Su definición no suele usarse para comparar conjuntos del mundo real.
Autosimilitud estadística de un fractal generado por el proceso de agregación por difusión limitada.

 Definición por algoritmos recursivos

Podemos destacar tres técnicas comunes para generar fractales:

 Aspectos matemáticos

 Intentos de definición rigurosa

El concepto de fractal no dispone en el año 2008 de una definición matemática precisa y de aceptación general. Intentos parciales de dar una definición fueron realizados por:
  • B. Mandelbrot, que en 1982 definió fractal como un conjunto cuya dimensión de Hausdorff-Besicovitch es estrictamente mayor que su dimensión topológica. Él mismo reconoció que su definición no era lo suficientemente general.
  • D. Sullivan, que definió matemáticamente una de las categorías de fractales con su definición de conjunto cuasiautosimilar que hacía uso del concepto de cuasi-isometría.

 Dimensión fractal

Artículo principal: Dimensión fractal
Puede definirse en términos del mínimo número N(ε) de bolas de radio ε necesarias para recubrir el conjunto, como el límite:
D_F=\lim_{\epsilon \to 0}{ \ln N(\epsilon) \over \ln(1/\epsilon)}
O en función del recuento del número de cajas Nn de una cuadrícula de anchura 1 / 2n que intersecan al conjunto:
D_F=\lim_{n \to \infty}{ \ln N_n \over \ln(2^n)}
Se demuestra que ambas definiciones son equivalentes, y que son invariantes bajo isometrías.[6]

 Dimensión de Hausdorff-Besicovitch

De una definición más compleja, la dimensión de Hausdorff-Besicovitch nos proporciona un número DH(A), también invariante bajo isometrías, cuya relación con la dimensión fractal DF(A) es la siguiente:
0 \leq D_H(A) \leq D_F(A)
Esto permite distinguir en algunos casos entre conjuntos con la misma dimensión fractal.

 Dimensión de fractales producidos por un IFS

En ese caso, cuando no haya solapamiento, se demuestra que DF = DH y que ambas pueden calcularse como solución de la ecuación:
c_1^D+c_2^D+ \dots + c_k^D=1
donde ci designa el factor de contracción de cada aplicación contractiva del IFS.

 Aplicaciones

Se han utilizado técnicas de fractales en la compresión de datos y en diversas disciplinas científicas.

 Compresión de imágenes

Fractal fern explained.png
Comprimir la imagen de un objeto autosemejante como el helecho de la figura no es difícil: haciendo uso del teorema del collage, debemos encontrar un IFS, conjunto de transformaciones que lleva la figura completa (en negro) en cada una de sus partes autosemejantes (rojo, azul celeste y azul marino). La información sobre la imagen quedará codificada en el IFS, y la aplicación reiterada de dichas transformaciones permite obtener la imagen procesada en cuestión.
Pero el enfoque anterior plantea problemas con muchas imágenes reales: no esperamos, por ejemplo, que la imagen de un gato presente pequeños gatitos distorsionados sobre sí mismo. Para solventarlo, en 1989 Arnaud Jacquin creó el esquema de sistemas de funciones iteradas particionadas: en él se subdivide la imagen mediante una partición y para cada región resultante se busca otra región similar a la primera bajo las transformaciones apropiadas.[7]
El esquema resultante es un sistema de compresión con pérdidas, de tiempo asimétrico. Lamentablemente aún se tarda mucho en encontrar las transformaciones que definen la imagen. No obstante, una vez encontradas, la descodificación es muy rápida. La compresión, aunque dependa de muchos factores, suele ser equiparable a la compresión JPEG, con lo cual el factor tiempo resulta determinante para decantarse por uno u otro sistema.

 Modelado de formas naturales

Fracción de un fractal Mandelbrot.
Las formas fractales, las formas en la que las partes se asemejan al todo, están presentes en la materia biológica, junto con las simetrías (las formas básicas que solo necesitan la mitad de información genética) y las espirales (Las formas de crecimiento y desarrollo de la forma básica hacia la ocupación de un mayor espacio), como las formas más sofisticadas en el desarrollo evolutivo de la materia biológica en cuanto que se presentan en procesos en los que se producen saltos cualitativos en las formas biológicas, es decir posibilitan catástrofes (hechos extraordinarios) que dan lugar a nuevas realidades más complejas, como las hojas que presentan una morfología similar a la pequeña rama de la que forman parte que, a su vez, presentan una forma similar a la rama, que a su vez es similar a la forma del árbol, y sin embargo cualitativamente no es lo mismo una hoja (forma biológica simple), que una rama o un árbol (forma biológica compleja).

 Sistemas dinámicos

Un atractor extraño: el Atractor de Lorenz.
Pero además las formas fractales no sólo se presentan en las formas espaciales de los objetos sino que se observan en la propia dinámica evolutiva de los sistemas complejos (ver teoría del caos). Dinámica que consta de ciclos (en los que partiendo de una realidad establecida simple acaban en la creación de una nueva realidad más compleja) que a su vez forman parte de ciclos más complejos los cuales forman parte del desarrollo de la dinámica de otro gran ciclo. Las evoluciones dinámicas de todos estos ciclos presentan las similitudes propias de los sistemas caóticos.

En manifestaciones artísticas

Imagen generada con el programa Apophysis.
Se usan tanto en la composición armónica y rítmica de una melodía como en la síntesis de sonidos. Esto se debe al uso de lo que en composición se llaman "micromodos", o pequeños grupos de 3 notas, a partir de los cuales uno puede trabajarlos de manera horizontal (melódica), o vertical (armónica). A su vez, el ritmo puede ser trabajado en sucesiones temporales especificas, que son determinadas por sucesiones de fractales.

 Literatura y poesía

Se usan también como punto de unión entre el arte y la ciencia, un ejemplo de eso es el científico-poeta chileno-alemán Mario Markus. En España, fue galardonado con el XI Premio de Poesía de la Academia de Poesía de Castilla y León, Fractalia, libro escrito por el poeta Carlos Escartín (Madrid, 1972), donde dedica este poemario a la exposición de cómo las Matemáticas y la Naturaleza están unidas desde el principio de los tiempos, y de cómo esto es posible actualmente verificarlo mediante el arte fractal, donde imágenes de la naturaleza (un copo de nieve, una hoja de un árbol) quedan perfectamente plasmadas en un plano, mediante la representación de puntos en el espacio realizados al aplicar algoritmos iterativos de números complejos.

 Artes gráficas

Con programas informáticos como Apophysis o Ultra Fractal se pueden hacer imágenes con técnicas diversas; cambiando parámetros, geometría de triángulos o con transformaciones aleatorias (a veces llamadas "mutaciones").

Referencias

  1. ↑ Benoît Mandelbrot, La Geometría Fractal de la Naturaleza, Tusquets, ISBN 84-8310-549-7
  2. ↑ Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd.. pp. XXV. ISBN 0-470-84862-6. 
  3. ↑ ¿Cuánto mide la costa de Gran Bretaña?
  4. ↑ Stewart, Ian. De aquí al infinito. Crítica, Grijalbo Mondadori, S.A., 1998. ISBN 84-7423-853-6.
  5. ↑ B. Mandelbrot. Los objetos fractales. Forma, azar y dimensión. Tusquets Editores, S.A., 1993. ISBN 978-84-7223-458-1
  6. ↑ Barnsley, M. Fractals everywhere.Academic Press Inc, 1988. ISBN 0-12-079062-9. (Cap 5)
  7. ↑ Jacquin, A.E.;Image coding based on a fractal theory of iterated contractive image transformations. Image Processing, IEEE Transactions on Volume 1, Issue 1, Jan. 1992 Page(s):18 - 30

 Véase también

 Enlaces externos

Arte fractal
Libros con licencia CC
Software
Vídeos
Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)